|
|

 |
|
補充資料 |
|
|
數學趣聞-化圓為方問題
|
化圓為方問題 |
化圓為方問題 (Problem of the quadrature of circle) 是二千四百多年前由古希臘人所提出的三大幾何作圖問題之一:作一正方形,使其面積和已知圓的面積相等。但古希臘要求的作圖工具為圓規和沒有刻度的直尺,使化圓為方問題的難度大增。
安納薩戈拉斯是最早研究化圓為方問題的人,他因「不敬神」的罪名被捕入獄。他在獄中鑽研化圓為方問題,遺憾地,他的成果到了最後失傳。其後更有希波克拉底、安提豐、希皮亞斯等著名的研者挑戰化圓為方問題,但終以失敗收場。
化圓為方問題曾吸引許多人研究,但無一成功。十九世紀有人證明了若設任意給定長度單位,則尺規可作的線段長必為代數數 。到了 1882 年,由法國數學家林德曼 (Von Lindemann) 證明了 p 是超越數,也同時解決了化圓為方問題以尺規作圖的不可能性。因為化圓為方問題相當於求作長為√p 的線段,但√p 並非代數數,因此尺規不可作。化圓為方問題由二千四百多年前的古希臘人提出,直到十九世紀才被解決,在數學史上經歷了二千三百多年。
化圓為方問題在數學史上經歷了二千三百多年,在這二千多年間,對數學界帶出了新的分支。希臘的安提豐為了解決化圓為方問題而提出的「窮竭法」是近代極限論的雛形。大意是指先作圓內接正方形(或正6邊形),然後每次 將邊數加倍,得內接8、16、32、…邊形,他相信「最後」的正多邊形必與圓周重合, 這樣就可以化圓為方了。雖然結論是錯誤的,但卻提供了求圓面積的近似方法,成為阿基米得 (Archimedes of Syracuse) 計算圓周率方法的先導,與中國劉徽的割圓術不謀而合,對窮竭法等科學方法的建立產生直接影響。
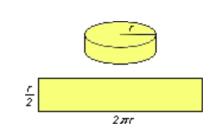
如果「化圓為方」這問題不局限於尺規作圖,它的解決方法有很多種。達‧芬奇 (Da Vinci) 用已知圓為底,圓半徑的一半為高的圓柱,在平面上滾動一周,所得的矩形,其面積恰好為圓的面積。
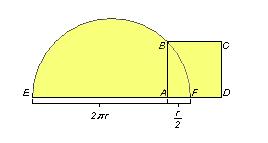
以 2 pr + r / 2 為直徑畫一個半圓形,在 A 點作一條與線段 EF 垂直的直線並與圓周相交於 B 點。然後再以 AB 為邊長作正方形 ABCD 。
根據畢氏定理(Pythagorean theorem),我們可以得出以下方程:
|
BE2 = AE2 + AB2 |
|
BF2 = AF2 + AB2 |
|
EF2 = BE2 + BF2 |
|
\EF2 = AE2 + AF2 + 2AB2 |
|
(2 pr + r / 2)2 = (2 pr)2 + (r / 2)2 + 2AB2 |
|
2AB2 = 2 pr2 |
|
\AB2 = pr2 |
以上証明了正方形 ABCD 的面積為 pr2 ,和已知圓的面積相等。雖然這方法的確把圓「化為方」,但讓圓柱在平面上滾動一周在尺規作圖中是不允許的,所以達‧芬奇並沒有真正解決化圓為方問題。
|
|
|
 |
|














